Центральный момент второго порядка есть. Числовые характеристики случайных величин

Рассмотрим дискретную случайную величину , заданную законом распределения:

Математическое ожидание равно:

Видим, что значительно больше . Это можно объяснить тем, что значение x = –150, намного отличающееся от остальных значений, при возведении в квадрат резко возросло; вероятность же этого значения мала (0,02). Таким образом, переход от M(X) к M(X 2) позволил лучше учесть влияние на математическое ожидание таких значений случайной величины, которые велики по абсолютной величине, но вероятность их появления мала. Разумеется, если бы величина имела несколько больших и маловероятных значений, то переход к величине X 2 , а тем более к величинам , и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины, причем не только дискретной, но и непрерывной.

Определение 6.10. Начальным моментом го порядка случайной величины называется математическое ожидание величины :

В частности:

Пользуясь этими моментами, формулу для вычисления дисперсии можно записать иначе

Кроме моментов случайной величины целесообразно рассматривать моменты отклонения .

Определение 6.11. Центральным моментом ого порядка случайной величины называется математическое ожидание величины .

(6.23)

В частности,

Легко выводятся соотношения, связывающие начальные и центральные моменты. Так, сравнивая (6.22) и (6.24), получим:

Нетрудно доказать и следующие соотношения:

Аналогично:

Моменты более высоких порядков используются редко. В определении центральных моментов используются отклонения случайной величины от ее математического ожидания (центра). Поэтому моменты называются центральными .

В определении начальных моментов также используются отклонения случайной величины, но не от математического ожидания, а от точки, абсцисса которой равна нулю, являющейся началом координат. Поэтому моменты называются начальными .

В случае непрерывной случайной величины начальный момент го порядка вычисляется по формуле:

(6.27)

Центральный момент го порядка непрерывной случайной величины вычисляется по формуле:

(6.28)

Предположим, что распределение случайной величины симметрично относительно математического ожидания. Тогда все центральные моменты нечетного порядка равны нулю. Это можно объяснить тем, что для каждого положительного значения величины X-M(X) найдется (в силу симметричности распределения относительно M(X) ) равное ему по абсолютной величине отрицательное значение этой величины, причем их вероятности будут одинаковыми.

Если центральный момент нечетного порядка не равны нулю, то это говорит об асимметричности распределения, причем чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент первого порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент третьего порядка.

Определение 6.12. Коэффициентом асимметрии называется величина:

Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину отрицательных отклонений. В этом случае кривая распределения (рис. 6.1а ) более полога слева от . Если коэффициент положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения более пологая справа.

Как известно, второй центральный момент (дисперсии) служит для характеристики рассеивания значений случайной величины вокруг ее математического ожидания. Если этот момент для некоторой случайной величины достаточно большой, т.е. рассеивание велико, то соответствующая кривая распределения более пологая, чем кривая распределения случайной величины, имеющей меньший момент второго порядка. Однако моментне может служить для этой цели в силу того, что для любого распределения .

В этом случае используется центральный момент четвертого порядка.

Определение 6.13. Эксцессом называется величина:

Для наиболее распространенного в природе нормального закона распределения отношение . Поэтому эксцесс, заданный формулой (6.28) служит для сравнения данного распределения с нормальным (рис. 6.1b ).

Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:

Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):

(6б )

Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.

Свойства математического ожидания:

Дисперсия. Дисперсией случайной величины Х называется число:

Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:

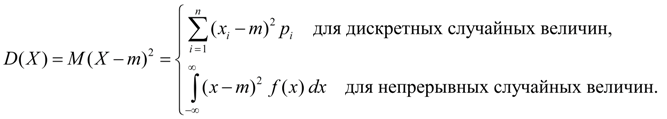(9)

Здесь m = М (Х ).

Свойства дисперсии:

Среднее квадратичное отклонение:

(11)

Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.

Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:

(12)

Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:

(13)

Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:

(14)

Из (7) следует, что центральный момент первого порядка всегда равен нулю:

Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С , а отклонение от центра не меняется: Х – m = (Х – С ) – (m – С ).
Теперь очевидно, что дисперсия – это центральный момент второго порядка :

Асимметрия. Центральный момент третьего порядка:

(17)

служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :

(18)

Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.

Эксцесс. Центральный момент четвертого порядка:

(19)

служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:

(20)

На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).

Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.

Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным . Если кривая распределения имеет более одного максимума, то распределение называется полимодальным . Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными . В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального , т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.

Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.

Особое значение для характеристики распределения случайной величины имеют числовые характеристики, называемые начальными и центральными моментами.

Начальным моментом k -го порядка α k (Х ) случайной величины Х k -ой степени этой величины, т.е.

α k (Х ) = М (Х k ) (6.8)

Формула (6.8) в силу определения математического ожидания для различных случайных величин имеет свой вид, а именно, для дискретной случайной величины с конечным множеством значений

для непрерывной случайной величины

, (6.10)

где f (x ) - плотность распределения случайной величины Х .

Несобственный интеграл в формуле (6.10) превращается в определенный интеграл по конечному промежутку, если значения непрерывной случайной величины имеются только в этом промежутке.

Одна из ранее введенных числовых характеристик – математическое ожидание – является не чем иным, как начальным моментом первого порядка, или, как говорят, первым начальным моментом:

М (Х ) = α 1 (Х ).

В предыдущем пункте было введено понятие центрированной случайной величины Х – М (Х ). Если эту величину рассматривать в качестве основной, то для нее также могут быть найдены начальные моменты. Для самой величины Х эти моменты будут называться центральными.

Центральным моментом k -го порядка μ k (Х ) случайной величины Х называется математическое ожидание k -ой степени центрированной случайной величины, т.е.

μ k (Х ) = М [(Х – М (Х )) k ] (6.11)

Иначе говоря, центральный момент k -го порядка – это математическое ожидание k -ой степени отклонения.

Центральный момент k -го порядка для дискретной случайной величины с конечным множеством значений находится по формуле:

, (6.12)

для непрерывной случайной величины по формуле:

(6.13)

В дальнейшем, когда будет понятно о какой случайной величине идет речь, то ее в обозначениях начальных и центральных моментах писать не будем, т.е. вместо α k (Х ) и μ k (Х ) будем писать просто α k и μ k .

Очевидно, что центральный момент первого порядка равен нулю, так как это ни что иное, как математическое ожидание отклонения, которое равно нулю по ранее доказанному, т.е. .

Нетрудно понять, что центральный момент второго порядка случайной величины Х совпадает с дисперсией этой же случайной величины, т.е.

Кроме этого, существуют следующие формулы, связывающие начальные и центральные моменты:

Итак, моменты первого и второго порядков (математическое ожидание и дисперсия) характеризуют самые важные черты распределения: его положение и степень разброса значений. Для более подробного описания распределения служат моменты более высоких порядков. Покажем это.

Предположим, что распределение случайной величины симметрично относительно своего математического ожидания. Тогда все центральные моменты нечетного порядка, если они существуют, равны нулю. Это объясняется тем, что в силу симметричности распределения для каждого положительного значения величины Х − М (Х ) существует равное ему по модулю отрицательное значение, при этом вероятности этих значений равны. Следовательно, сумма в формуле (6.12) состоит из нескольких пар, равных по модулю, но разных по знаку слагаемых, которые при суммировании взаимно уничтожаются. Таким образом, вся сумма, т.е. центральный момент любого нечетного порядка дискретной случайной величины равен нулю. Аналогично, центральный момент любого нечетного порядка непрерывной случайной величины равен нулю, как интеграл в симметричных пределах от нечетной функции.

Естественно предположить, что если центральный момент нечетного порядка отличен от нуля, то и само распределение не будет симметрично относительно своего математического ожидания. При этом, чем больше центральный момент отличается от нуля, тем больше асимметрия в распределении. Возьмем в качестве характеристики асимметрии центральный момент наименьшего нечетного порядка. Так как центральный момент первого порядка равен нулю для случайных величин, имеющих любые распределения, то для этой цели лучше использовать центральный момент третьего порядка. Однако этот момент имеет размерность куба случайной величины. Чтобы избавиться от этого недостатка и перейти к безразмерной случайной величине, делят значение центрального момента на куб среднеквадратического отклонения.

Коэффициентом асимметрии А s или просто асимметрией называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения, т.е.

Иногда асимметрию называют "скошенностью" и обозначают S k , что происходит от английского слова skew – "косой".

Если коэффициент асимметрии отрицательный, то на его величину достаточно сильно влияние отрицательных слагаемых (отклонений) и распределение будет иметь левую асимметрию , а график (кривая) распределения является более пологим слева от математического ожидания. Если коэффициент положителен, то асимметрия правая , а кривая более полога справа от математического ожидания (рис.6.1).

Как было показано, для характеристики разброса значений случайной величины вокруг своего математического ожидания служит второй центральный момент, т.е. дисперсия. Если этот момент имеет большое числовое значение, то данная случайная величина имеет большой разброс значений и соответствующая кривая распределения имеет более пологий вид, чем кривая, для которой второй центральный момент имеет меньшее значение. Поэтому второй центральный момент характеризует, в какой-то степени, "плосковершинность" или "островершинность" кривой распределения. Однако эта характеристика не очень удобная. Центральный момент второго порядка имеет размерность равную квадрату размерности случайной величины. Если попытаться получить безразмерную величину, поделив значение момента на квадрат среднеквадратического отклонения, то для любой случайной величины получим: . Таким образом, этот коэффициент не может являться какой-либо характеристикой распределения случайной величины. Он одинаков для всех распределений. В этом случае можно использовать центральный момент четвертого порядка.

Эксцессом E k называется величина, определяемая по формуле

(6.15)

Эксцесс, в основном, применяется для непрерывных случайных величин и служит для характеристики, так называемой "крутости" кривой распределения, или иначе, как уже было сказано, для характеристики "плосковершинности" или "островершинности" кривой распределения. В качестве эталонной кривой распределения считается кривая нормального распределения (о нем будет подробно идти речь в следующем главе). Для случайной величины, распределенной по нормальному закону, имеет место равенство . Поэтому эксцесс, заданный формулой (6.15), служит для сравнения данного распределения с нормальным, у которого эксцесс получается равным нулю.

Если для какой-то случайной величины получен положительный эксцесс, то кривая распределения этой величины является более островершинной, чем кривая нормального распределения. Если же эксцесс отрицателен, то кривая является более плосковершинной по сравнению с кривой нормального распределения (рис. 6.2).

Перейдем теперь к конкретным видам законов распределения дискретной и непрерывной случайных величин.

Центральными называются моменты распределения, при вычислении которых за исходную величину принимаются отклонение вариантов от средней арифметической данного ряда.

1. Рассчитаем центральный момент первого порядка по формуле:

2. Рассчитаем центральный момент второго порядка по формуле:

где - значение середины интервалов;

Это среднее взвешенное;

Fi-число значений.

3. Рассчитаем центральный момент третьего порядка по формуле:

где - значение середины интервалов; - это среднее взвешенное; - fi-число значений.

4. Рассчитаем центральный момент четвертого порядка по формуле:

где - значение середины интервалов; - это среднее взвешенное; - fi-число значений.

Расчет для таблицы 3.2

Расчет для таблицы 3.4

1. Рассчитаем центральный момент первого порядка по формуле (7.1):

2. Рассчитаем центральный момент второго порядка по формуле (7.2):

3. Рассчитаем центральный момент третьего порядка по формуле (7.3):

4. Рассчитаем центральный момент четвертого порядка по формуле (7.4):

Расчет для таблицы 3.6

1. Рассчитаем центральный момент первого порядка по формуле (7.1):

2. Рассчитаем центральный момент второго порядка по формуле (7.2):

3. Рассчитаем центральный момент третьего порядка по формуле (7.3):

4. Рассчитаем центральный момент четвертого порядка по формуле (7.4):

Рассчитаны моменты 1,2,3,4 порядков по трем задачам. Где момент третьего порядка понадобиться для расчета асимметрии, а момент четвертого порядка понадобиться для расчета эксцесса.

РАСЧЕТ АСИММЕТРИИ РАСПРЕДЕЛЕНИЯ

В статистической практике встречаются разнообразные распределения. Различают следующие разновидности кривых распределения:

· одновершинные кривые: симметричные, умеренно асимметричные и крайне асимметричные;

· многовершинные кривые.

Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух или более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает оценку его однородности, а также вычисление показателей асимметрии и эксцесса. Для симметричных распределений частоты любых двух вариант, равностоящих в обе стороны от центра распределения, равны между собой. Рассчитанные для таких распределений средняя, мода и медиана также равны.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии ():

где -это среднее взвешенное; Mo-мода; -среднеквадратичная взвешенная дисперсия; Me-медиана.

Его величина может быть положительной и отрицательной. В первом случае речь идет о правосторонней асимметрии, а во втором- о левосторонней.

При правосторонней асимметрии Mo>Me >x. Наиболее широко (как показатель асимметрии) применяется отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе:

где -центральный момент третьего порядка; -среднее квадратическое отклонение в кубе.

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной; если она меньше 0,25, то незначительной.

Оценка существенности производится на основе средней квадратической ошибки, коэффициента асимметрии (), которая зависит от числа наблюдений (n) и рассчитывается по формуле:

где n-число наблюдений.

В случае асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами.

Расчет для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.

Левосторонняя, значительная асимметрия.

Расчет для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.

1. Определим асимметрии по формуле (7.5):

Правосторонняя, значительная асимметрия.

Расчет для таблицы 3.6 Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)

1. Определим асимметрии по формуле (7.5):

Правосторонняя, незначительная асимметрия.

РАСЧЕТ ЭКСЦЕССА РАСПРЕДЕЛЕНИЯ

Для симметричных распределений может быть рассчитан показатель эксцесса ():

где - центральный момент четвертого порядка; - средне квадратическое отклонение в четвертой степени.

Расчет для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.

Расчет для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.

Рассчитаем показатель эксцесса по формуле (7.7)

Островершинное распределение.

Рассчитаем показатель эксцесса по формуле (7.7)

Плосковершинное распределение.

ОЦЕНКА ОДНОРОДНОСТИ СОВОКУПНОСТИ

Оценка однородности для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб.

Необходимо отметить, что хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определенные указания для дальнейшего исследования социально - экономических явлений. Полученный результат свидетельствует о наличии значительной по величине и отрицательной по своему характеру асимметрии, нужно заметить, что асимметрия является левосторонней. Кроме того совокупность имеет плос-ковершинное распределение.

Оценка однородности для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб.

Полученный результат свидетельствует о наличии значительной по величине и положительной по своему характеру асимметрии, нужно заметить что асимметрия является правосторонней. А так же совокупность имеет остро-вершинное распределение.

Оценка однородности для таблицы 3.6 Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)

Полученный результат свидетельствует о наличии незначительной по величине и положительной по своему характеру асимметрии, нужно заметить что асимметрия является правосторонней. Кроме того совокупность имеет плосковершинное распределение.

Для характеристики различных свойств случайных величин используются начальные и центральные моменты.

Начальным моментом k- го порядка случайной величины Х называется математическое ожидание k-й степени этой величины:

α К = М .

Для дискретной случайной величины

Х = Х – М[Х]

ентрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:

Условимся отличать центрированную с.в. значком 0 наверху.

Центральным моментом S -го порядка называется математическое ожидание S-й степени центрированной случайной величины

 S = M [(X – m x) S ].

Для дискретной случайной величины

 S = (x i – m x) S p i .

Для непрерывной случайной величины

Свойства моментов случайных величин

начальный момент первого порядка равен математическому ожиданию (по определению):

α 1 = М = m x .

центральный момент первого порядка всегда равен нулю (докажем на примере дискретной с. в.):

 1 = M [(X – m x) 1 ] =(x i – m x) p i =x i p i –m x p i = m x –m x p i =m x –m x = 0.

центральный момент второго порядка характеризует разброс случайной величины вокруг ее математического ожидания.

Центральный момент второго порядка называется дисперсией с. в. и обозначается D[X] или D x

Дисперсия имеет размерность квадрата случайной величины.

Среднее квадратическое отклонение σ х = √D x .

σ х – также как и D x характеризует разброс случайной величины вокруг ее математического ожидания но имеет размерность случайной величины.

второй начальный момент α 2 характеризует степень разброса случайной величины вокруг ее математического ожидания, а также смещение случайной величины на числовой оси

Связь первого и второго начальных моментов с дисперсией (на примере непрерывной с. в.):

третий центральный момент характеризует степень разброса случайной величины вокруг математического ожидания, а также степень асимметрии распределения случайной величины.

f(x ср) > f(-x ср)

Для симметричных законов распределения m 3 = 0.

Для характеристики только степени асимметрии используется так называемый коэффициент асимметрии

Для симметричного закона распределения Sk = 0

четвертый центральный момент характеризует степень разброса случайной величины вокруг математического ожидания, а также степень островершинности закона распределения.